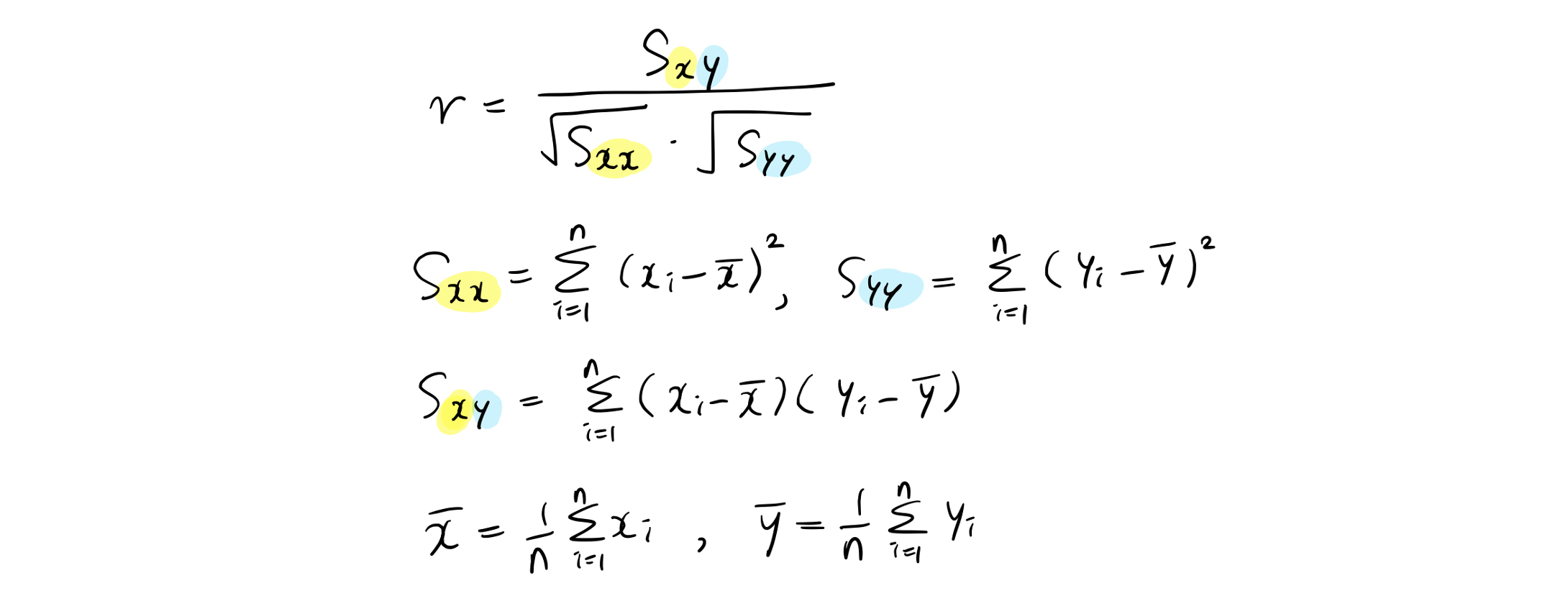[NLP] Similarity Measures (유사도 측정)
by Heejin Do
자연어처리에서 유용하게 쓰일 수 있는, 문서/벡터 간 유사도를 측정하는 기법들을 간단히 정리해보았다.
1. Euclidean Distance (유클리드 거리)
유클리드 거리는 두 점 사이의 거리를 계산하며, 두 점 $p=(p_{1}, p_{2}, …, p_{n})$과 $q=(q_{1}, q_{2}, …, q_{n})$ 사이의 유클리드 거리를 구하는 구체적인 식은 아래와 같다.
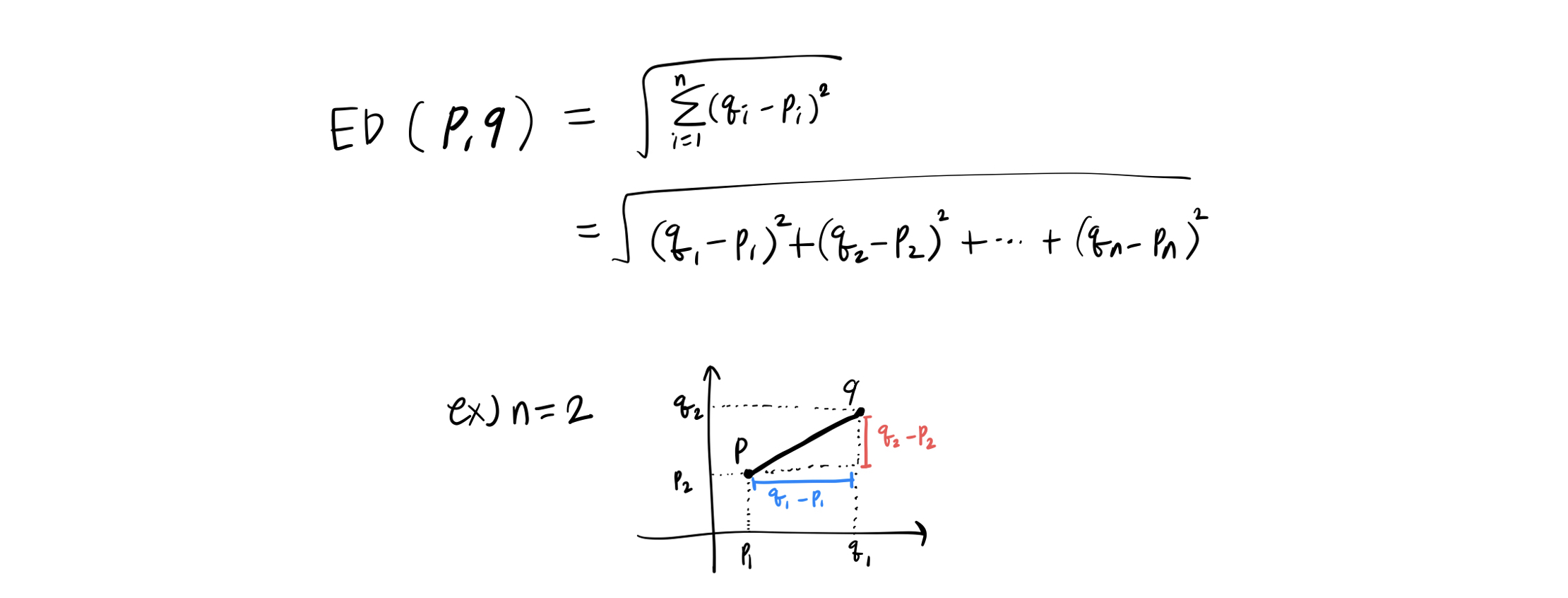
- 값이 클수록 두 문서간 거리가 멀다.
2. Jaccard Similarity (자카드 유사도)
자카드 유사도는 두 집합 간 겹치는 요소의 비율로 계산한다. 구체적으로, 두 집합의 합집합 중 교집합의 비율을 계산하며, 0에서 1 사이의 값을 가진다.
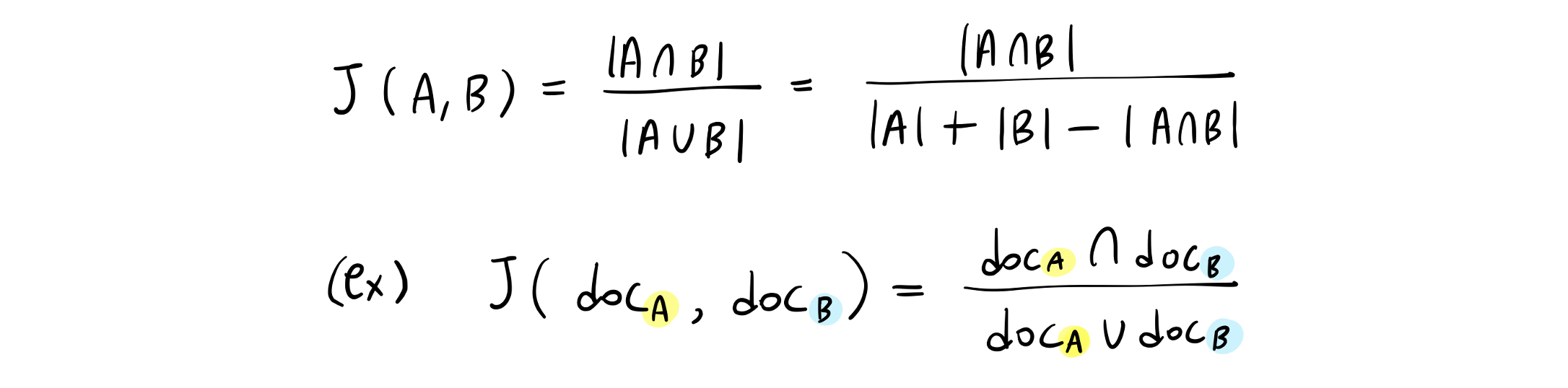
$doc_{A}$ = {‘Look’, ‘at’, ‘the’, ‘moon’, ‘.’}
$doc_{B}$ = {‘The’, ‘moon’, ‘is’, ‘so’, ‘pretty’, ‘.’}
$Jaccard(A,B) = 3/8$
- 값이 클수록 두 문서간 거리가 가깝다.
- 간단하지만, 단어의 발생 빈도(frequency)를 고려하지 못한다는 단점이 있다.
3. Cosine Similarity (코사인 유사도)
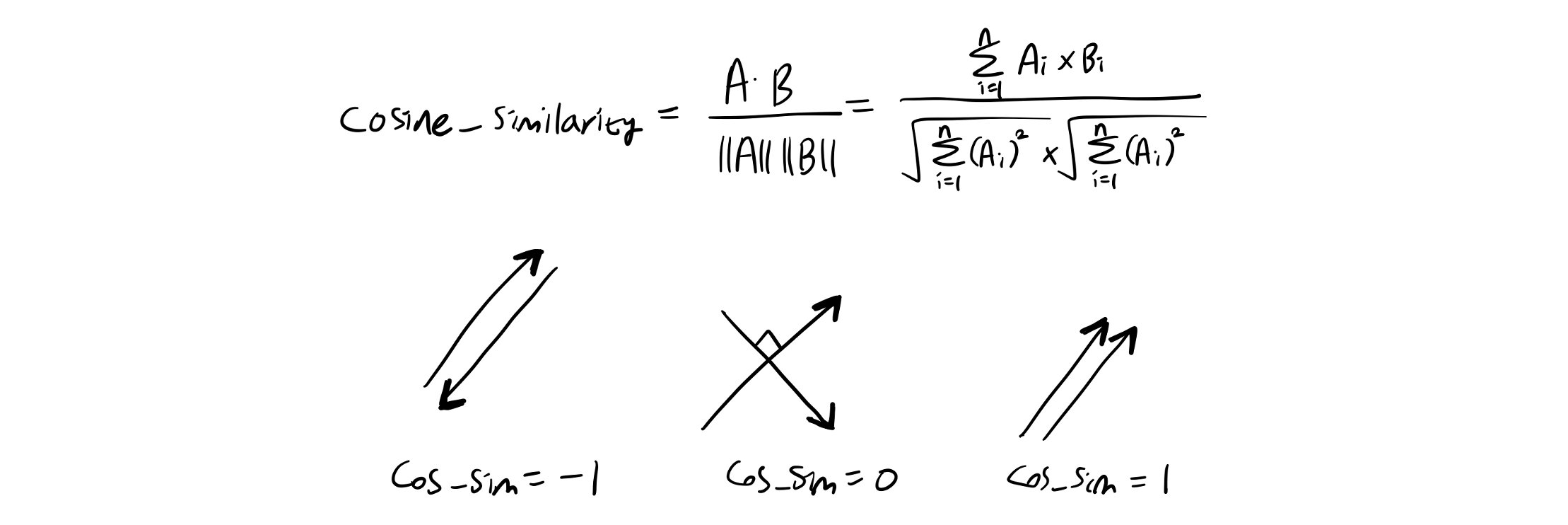
코사인 유사도는 두 벡터 간의 코사인 각도를 이용하여 계산하며, 벡터의 실제 위치가 아닌 방향의 유사도를 측정한다. -1에서 1까지의 값을 가지며 두 벡터 $A$ 와 $B$ 간의 코사인 유사도를 계산하는 구체적인 수식은 아래와 같다.
- 값이 클수록 두 문서(벡터)의 방향이 유사하다.
- 벡터의 크기와 관계없이 유사도를 측정할 수 있지만, 위치 벡터의 기준에 따라 유사도 값에 차이가 발생한다는 단점이 있다.
4. Correlation Coefficient(상관계수)
상관계수는 두 변수 간 선형관계의 정도를 나타내는 계수이다. 피어슨 (Pearson) 상관계수라고도 부르며 -1에서 1까지의 값을 가진다. 상관계수의 크기는 얼마나 직선값에 가까운지를, 부호는 직선관계의 방향을 의미한다.
- 상관계수의 값(절대값)이 클수록 두 변수 사이 상관성이 크며, - 부호일 경우 양의 상관성, + 부호의 경우 음의 상관성을 가진다.
- 상관계수의 값이 0에 가까울수록 두 변수 간 연관성이 작다.
Subscribe via RSS